Магические квадраты были  известна людям и в древность.    Наибольшую известность получил квадрат средневекового художника Дюрера, помещенный им на полотне сложной абстрактной картины «Меланхолия».

     Со временем магические квадраты стали популярны. Они завораживают своей   непонятной правильностью. Поэтому  составлением магических квадратов увлекались, и продолжают увлекаться, как ученые, так и школьники.

   Найдена математическая константа, определены различные методы построения магических квадратов. А количество их огромно! Подсчитано, что квадратов  4 на 4 можно построить 880, а квадратов 5 на 5 - уже около четверти миллиона. Количество квадратов большего порядка, вообще, для нашего сознания беспредельно.

 

   Но что такой магический квадрат для современной европейской математики? Всего лишь интересная задачка, гимнастика для ума. Построен квадрат – и задачка решена. Но там, где европейская индуктивная математика свою работу заканчивает, там дедуктивная  законопознавательная математика к работе только приступает!

   Дедуктивная математика  добавляет в магические квадраты линии со стрелками. Право направленная стрелка – это мужское движение, раскручивающееся. Лево направленное движение – женское - сворачивающееся. Появляются модели. Они простые, абстрактные. Но их много, они непрерывно меняются, то есть  переходят в модели другие. И сама линия имеет не только направление, но и постоянную скорость, и структуру, также непрерывно меняющуюся.

 

   Исследуя модели магических квадратов можно многое понять в устройстве мира! (А дедуктивная математика никогда не забывает о своей главной задаче – объяснить строение мира.) Прежде всего, магические квадраты показывают Космическое Движение! Однородность  – одинаковость, а значит и пустота Все линии магических квадратов (от стенки-до стенки) однородны – в них одинаковое количество космических точек – энергии. Но отдельные части этих линий  (в клетках)– это набор  неповторимых чисел.  А число- это и модель! И в каждой единице, на самом деле, уже стоит  громадное число энергерических точек. И между двумя последовательными числами-клеточками   (например, 1 и 2) тоже что-то структурное стоит…

 

    Простейший квадрат -  3 на 3 дает только одну модель. Но единица может содержать в себе любое число. К тому же, прибавление можно заменить возведением в квадрат, и модель при этом не изменится.

Из квадратов 4 на 4 квадрат Дюрера самый красивый и «правильный». Он лучше всего иллюстрирует Космическое Движение.

   Другие магические квадраты 4 на 4 тоже какие-то модели в себе содержат. Меньше становится линий, проходящих через все поле квадрата, появляются замкнутые участки, где энергия циркулирует по кругу. Но в мире-Космосе  все эти модели должны существовать в виде реальности!

  

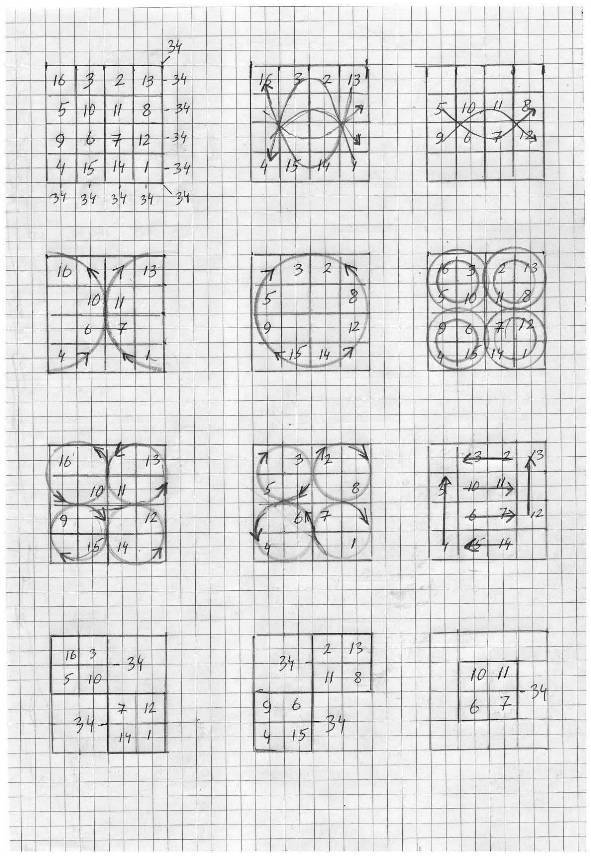
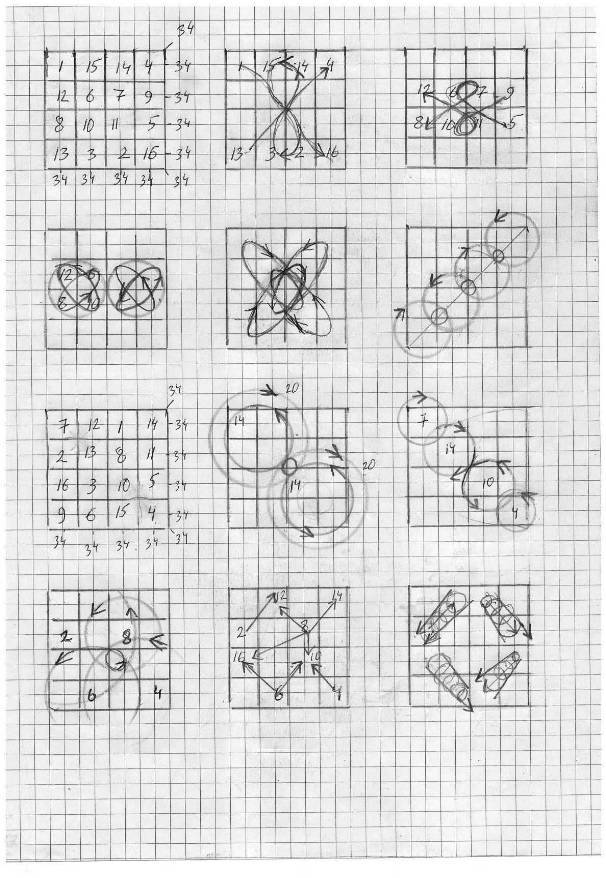
Перестановка двух рядов не изменила суммы сторон, но создала иную модель

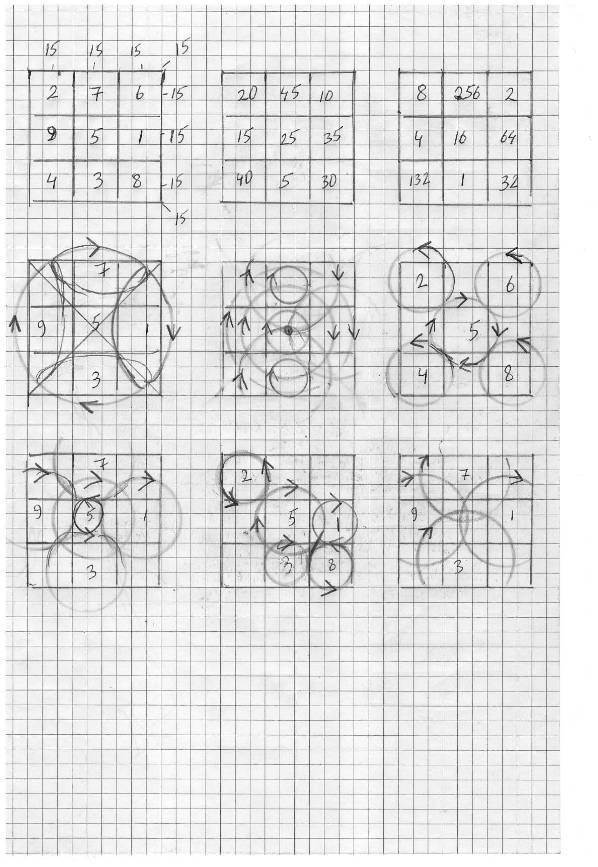
       Простейший               квадрат